Theory
Magnetostrophic theory
We are working on the underlying theory of magnetostrophic balance, namely the dynamics resulting from a balance between Coriolis forces, pressure gradients, Lorentz (magnetic) forces and buoyancy. This corresponds to the zero Rossby number, zero Ekman number limit examined by J.B. Taylor in his famous 1963 paper external page"The Magneto-Hydrodynamics of a Rotating Fluid and the Earth's Dynamo Problem"call_made.
The neglect of inertial terms in the Navier-Stokes equations is well-founded: the magnetic Rossby number, measuring the ratio of the rotational timescale to the magnetic dissipation timescale, is very small, of order 10-9; and the Ekman number, measuring the ratio of the rotational timescale to the viscous dissipation timescale, is also very small, on the order of 10-15 (these numbers all result from taking the size of the core as the relevant length scale). Indeed, the famous 3-D self-consistent dynamo simulations of Glatzmaier and Roberts in 1995 neglected inertia. This in itself presents no difficulties. What does cause difficulties is the simultaneous neglect of both inertia and viscosity. This leads to the famous "Taylor constraint'' which says that the azimuthal torque averaged over every cylinder coaxial with the rotation axis must vanish. One of the difficulties here is the word "every'': there are, in principle, an infinite number of constraints that must apply to the system.
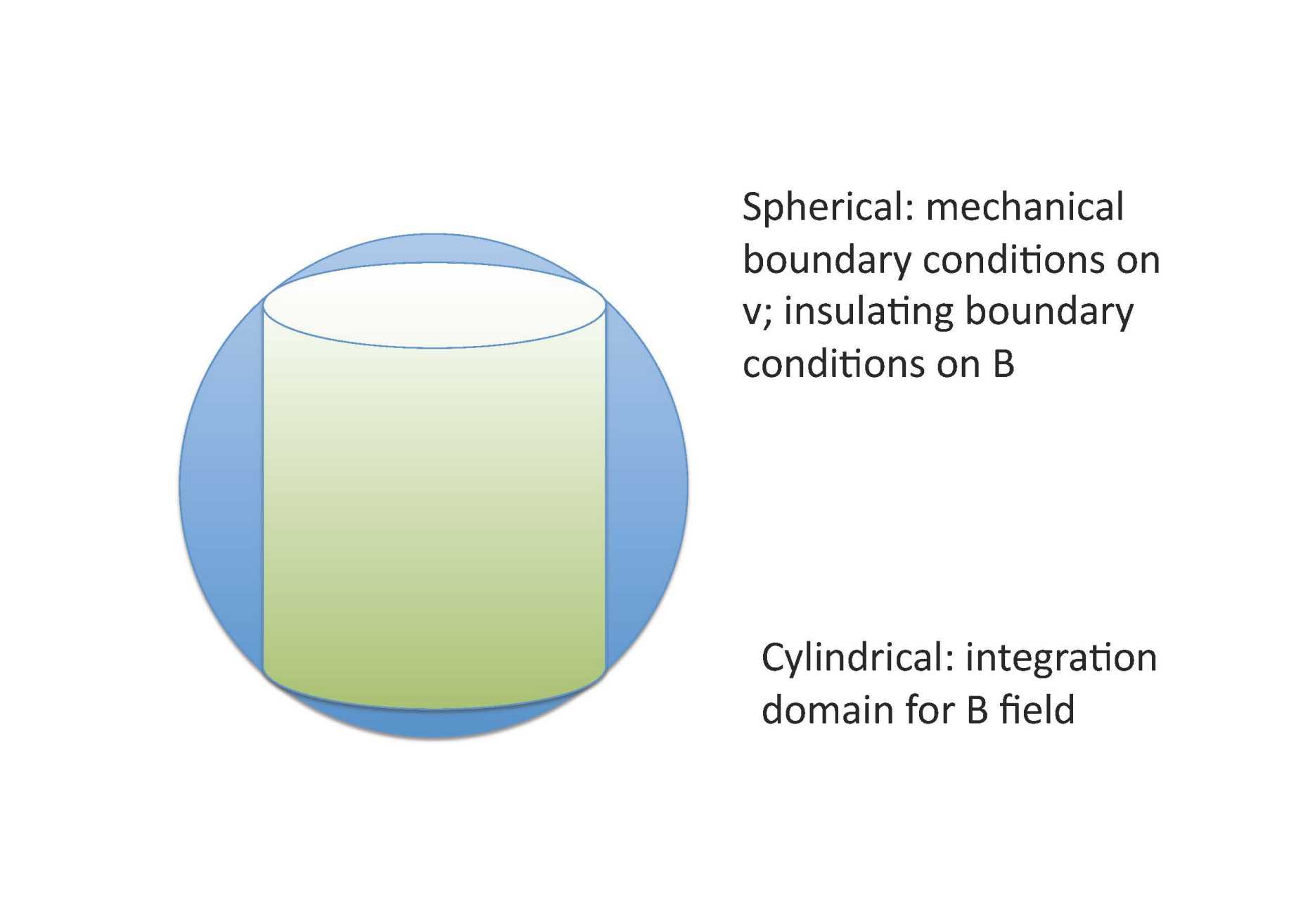
One challenge is the accurate calculation of integrals over cylinders in what is an inherently spherical system: we need both spherical and cylindrical coordinates (see Figure 1).
The accurate computation is accomplished when we use a special polynomial expansion of the underlying magnetic fields (and thus the Lorentz torques) in terms of spherical harmonics and a type of Jacobi polynomial in radius. Then the integrals can be performed exactly. A second benefit of this representation is that the infinite set of constraints (cylindrical integrals) becomes finite and countable.
Together with Philip Livermore and Glenn Ierley we have developed much of the requisite machinery to handle these constraints. We continue to work on time-stepping schemes that honour the Taylor constraints at every time-step. The ultimate goal is a new kind of numerical dynamo model which is not limited by viscosity, as is the case in current models of the dynamo.
Relevant papers:
Jackson, Livermore and Ierley, PEPI, Vol. 187 (3-4), pp. 322-327, 2011.
Livermore, Ierley and Jackson, GJI, Vol. 187 (2), pp. 690-704, 2011.
Scaling laws
The magnetic field of the Earth is generated by motions of an electrically conducting fluid in the outer core, consisting mainly of liquid iron. It is important for navigation and it shields our planet from the high-energy charged particles of the solar wind. Thus the geomagnetic field appears to be an important ingredient to support life. A third point why the core is a central part of the Earth is that it supplies the heat at the base of the mantle. In that way, it is at least partly responsible for mantle convection and plate tectonics. Hence it is essential for the study of the system Earth to determine the state and the processes of the core.
It is, however, not possible to study Earth's core by means of direct observations. Also the use of remote observations, e.g. of the geomagnetic field, for the determination of the dynamics of the outer core is limited.
It is generally accepted that the fluid motions in the outer core, which are most important for maintaining the geodynamo, are driven by convection, i.e. by thermal and compositional buoyancy forces (Olson in Treatise on Geophysics, 2007).
One way of studying the dynamics of the outer core is to model the whole system numerically on the basis of the governing physical equations. The five fundamental equations solved in dynamo models are the Navier-Stokes equation in a rotating frame including the Lorentz force, the induction and temperature equations, as well as constraints on the velocity and the magnetic field. Starting with the fi rst successful 3D MHD (magneto-hydrodynamic) self-sustained dynamo model of Glatzmaier and Roberts (1995), numerical dynamo simulations were able to reproduce various features of the geomagnetic fi eld like field morphology, secular variations and polarity reversals. Although it seems that the dynamics of the core could be similar to these models, the problem remains how to apply them to the Earth. A major point is the discrepancy between the numerical models and the Earth's core in terms of the dimensionless parameters. In particular, numerical dynamos have far too slow rotation (Ekman number too large), are less turbulent (Rayleigh number too small) and excessively viscous relative to their electrical conductivity (magnetic Prandtl number too large) compared to the core. This gap can not be bridged easily due to the enormous computational power required to resolve all relevant time and length scales.
Assuming that the relevant processes in Earth's core and in the dynamo models are the same, we can extrapolate the results from the numerics to the parameter range of the core. But what are reasonable laws that describe the scaling behaviour of quantities like heat transport, flow velocity and magnetic field strength correctly?
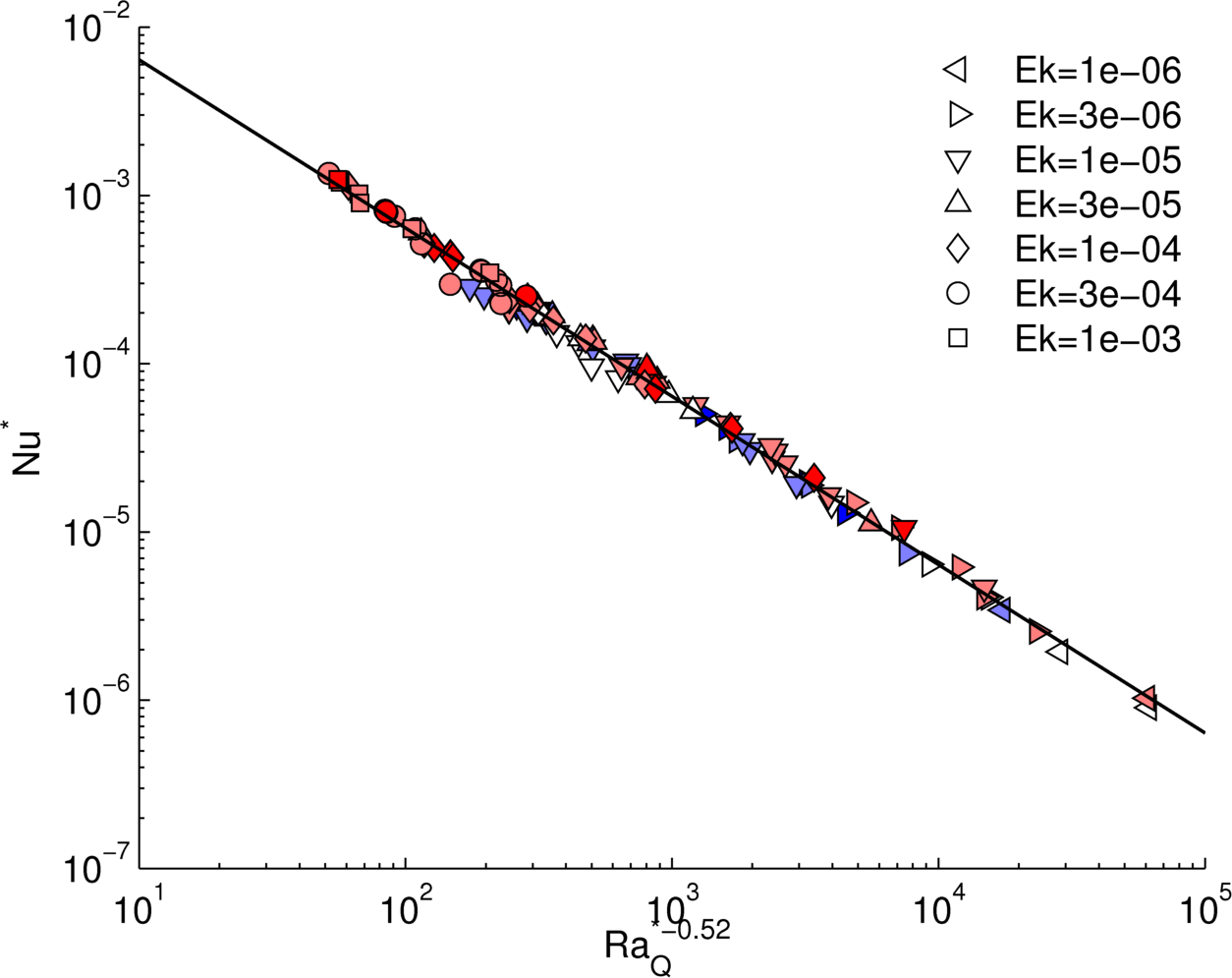
Intrigued by the work of Christensen and co-workers who proposed simple diffusivity-free scaling relations, we study the support of different laws by the data. This problem is a classical problem of model selection. How many parameters are needed to account for the variability in the data? To find an answer to this question, we use statistical methods from the areas of frequentist and Bayesian statistics. Eventually we focussed on cross-validation which estimates the performance of a predictive model. For most cases, our analysis does not support diffusivity-free scaling laws (Stelzer & Jackson, 2013, submitted).